A Car on a Fragile Bridge
A car is crossing a 20km long bridge. The bridge can support at most
1500kg of weight over it. If somehow, the weight on the bridge becomes
more than that, it will break.
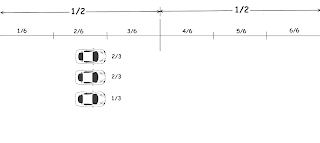
Now, the weight of the car is exactly 1500kg. At the midway, a bird comes and sits on the roof of the car. This bird weighs exactly 200 gram.
Can you tell if the bridge breaks at this point or not?
Read what will happen next?
Source
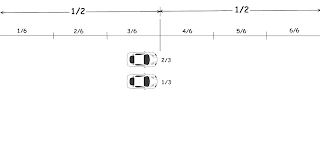
Now, the weight of the car is exactly 1500kg. At the midway, a bird comes and sits on the roof of the car. This bird weighs exactly 200 gram.
Can you tell if the bridge breaks at this point or not?
Read what will happen next?
Source